See the original problem on HackerRank.

Warning: HackerRank has recently changed the constraints of the problem by allowing duplicates. This change invalidated a couple of our solutions. This is discussed in the post.

Solutions

We found many solutions to this challenge.

Naive solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

bool isBeautiful(int i, int j, int k, int d, const vector<int>& arr) {
    int a = arr[j] - arr[i];
    int b = arr[k] - arr[j];
    return a == b && a == d;
}

int beautifulTriplets(int d, vector<int> arr) {
    int n = arr.size();
    int count = 0;
    for (int i = 0; i != n; ++i) {
        for (int j = 0; j != n; ++j) {
            for (int k = 0; k != n; ++k) {
                count += isBeautiful(i,j,k,d, arr);
            }
        }
    }
    return count;
}

The brute force \( O(N^3) \) solution does not work for all the test cases, so we need to somehow exploit the structure of the problem.

Our solutions are based on the observation that given an element of the triplet we can easily search for the other two, given that:

\( a_j - a_i = a_k - a_j = d \)

So if we go over all the elements and imagine to have found \( a_i \), we can seek \( a_j \) as \( a_i + d \) and \( a_k \) as \( a_i + 2d \).

Binary Search

Since the sequence is increasing, we can use a binary search:

1
2
3
4
5

auto dd = d + d;
cout << count_if(begin(v), end(v), [&](auto i){
          return binary_search(begin(v), end(v), i+d) &&
                 binary_search(begin(v), end(v), i+dd);
        });

Smarter Binary Search

A possible optimization works only on the original version of the problem: no duplicates allowed (the sequence is always increasing).

We reduce the span of the two binary searches: as you see, in the code above we do two binary searches on the whole array every time. Instead of seeking for \( a_j \) and \( a_k \) we can imagine to have found \( a_j \) and seek \( a_i \) and \( a_k \). Since \( a_i \) has to be on the left and \( a_k \) on the right, \( j \) becomes a sort of pivot and cuts the search space:

1
2
3
4
5
6
7

auto cnt = 0;
for (auto j=0; j<n; ++j)
{
    cnt += binary_search(begin(v), begin(v)+j, v[j]-d) &&
           binary_search(begin(v)+j, end(v), v[j]+d);
}
cout << cnt;

Clearly, the solution above does not work correctly when duplicates are in the array because for any \(a_j\) we can have more than one \(a_i\) and/or \(a_k\).

Functional-style Not-so-brute Force Search

Rewriting the concepts of the previous solutions, we can write a more efficient, but still more or less brute-force approach. However, this solution is fast enough to pass all the tests.

Like many functional expression, this one is better when commented inline:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

// take all the tails, that is all the lists obtained removing the initial elements one at a time
arr.tails
  // take only those with enough elements
  .filter(_.length >= 3)
  // keep only the interesting elements; beyond that they can't be part of the triplet
  .map { l => l.takeWhile(_ <= l.head + d * 2) }
  // find how many second and third elements of the triplet are there, if any.
  // combining them (that is, multiplying their quantities) we found how many triplets are possible with the current initial element 
  .map { sh =>
    sh.count(_ == (sh.head + d)) * sh.count(_ == (sh.head + 2 * d))
  }
  // sum all the triplets found
  .sum

Reducing the number of elements in the intermediate lists cuts the constant part of the O(N^3) complexity of this implementation enough to pass all the test. The worst case for this algorithm would be a very large number of identical elements, that would make the takeWhile operation ineffective.

Anyway, this implementation passes all the tests, and correctly manages duplicate elements.

Linear (not in general)

If the problem does not allow duplicates, we can exploit the fact that \( d \) is small (at most 20). Then for each beautiful triplet the distance between \( a_i \) and \( a_k \) is 2d. This means that found \( a_i \), we can seek \( a_j \) and \( a_k \) at most in 40 steps. This results in a constant for the problem.

Notice that the value of \( d \) is small, and recall that the input will always be in increasing order; because the input must be increasing, then a valid \( a_j \) will never be more than \( d \) indices to the right of \( a_i \), and a valid \( a k \) will never be more than \( d \) indices to the right of a valid \( a_j \) (or \( 2 \times d \) indices to the right of a corresponding \( a_j \). So, for each \( a_i \), the value \( a_j + d \) can only exist between indices \( i \) and \( i + d \) m and the value \( a_i + d + d\) can only exist between index \( i \) and index \( a_i + d + d\). You can just loop over this reduced range and check if the values exist.

So, the following code is linear:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

auto cnt = 0;
for (auto i=0; i<n; ++i)
{
    auto found = 0;
    for (auto j=i+1; j<min(n, i+d+d+1); ++j)
    {
        if (v[j]-v[i] == d)
            ++found;
        if (v[j]-v[i] == (d+d))
            ++found;
    }
    cnt += (found == 2);
}
cout << cnt;

Or in python:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

n, d = map(int , raw_input().split())
a = map(int , raw_input().split())

ans = 0
for i in range(n):
    found = 0
    for j in range(i + 1, min(i + d + d + 1, n)):
        if a[j] - a[i] == d:
            found=found+1
        if a[j] - a[i] == d + d:
            found = found + 1
    if found == 2:
        ans = ans + 1
print ans

Clearly we are exploiting a shortcut of the problem here. If \( d \) grows to \( N \), the solution turns into quadratic.

Really Linear

A 100% linear solution (working with duplicates too) comes with extra space. You know, sometimes space and time are interchangeable. To get rid of the lookup time, we can use a frequency table to store if a certain number occurs. This way seeking for any number (e.g. \( a_i + d \)) would result in constant time, reducing the total cost to \( O(N) \) (we still need to iterate all the elements):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

int main() 
{
    static constexpr int max_n = 20000;
    int n, d;
    std::cin >> n >> d;

    std::vector<int> v(n);
    std::copy_n(std::istream_iterator<int>(std::cin), n, v.begin());

    std::array<bool, max_n + 1> freq{};
    for (auto val : v)
        freq[val] = true;
    
    std::cout << std::count_if(v.begin(), v.end(), [&](int val) {
        const int dd = val + d + d;
        return (dd <= max_n) && freq[val + d] && freq[dd];
    });
}

We can afford this solution because the domain is quite little.

We may use std::unordered_set to save some space. std::unordered_set is implemented with hash set (average constant-time complexity). But, depending on the input, we may waste most of the time creating the set.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

int main() 
{
    int n, d;
    std::cin >> n >> d;

    std::vector<int> vec(n);
    std::copy_n(std::istream_iterator<int>(std::cin), n, vec.begin());
    std::unordered_set<int> set(vec.begin(), vec.end());

    int result = std::count_if(vec.begin(), vec.end(), [&](int val) {
        return set.count(val + d) && set.count(val + d + d);
    });

    std::cout << result << "\n";
}

A similar approach in Python:

1
2

nums = set(arr)
return sum(n + d in nums and n + d + d in nums for n in arr)

Frequency table with patterns

Another way of seeing the solution with a frequency table is thinking in terms of “sliding windows”.

Suppose we have this frequency table:

1

[0, 2, 1, 0, 1, 1, 0, 1, 1, 0, 2]

Where the first element is the freqency of 0. Suppose d=3.

Beautiful triplets are all triplets at a distance d. We can set a “sliding window” at the elements:

1
2
3

f[0]    -> 0
f[d]    -> 0
f[d+d]  -> 0

This means we do not have such a triplet.

Then we move the window by one position:

1
2
3

f[1]      -> 2
f[d+1]    -> 1
f[d+d+1]  -> 1

In this case we find something. In particular, we can do \(2 \cdot 1 \cdot 1\) triplets.

And so on.

Do you see the pattern?

It’s like zipping the frequency table with itself shited by d and with itself shifted by d+d:

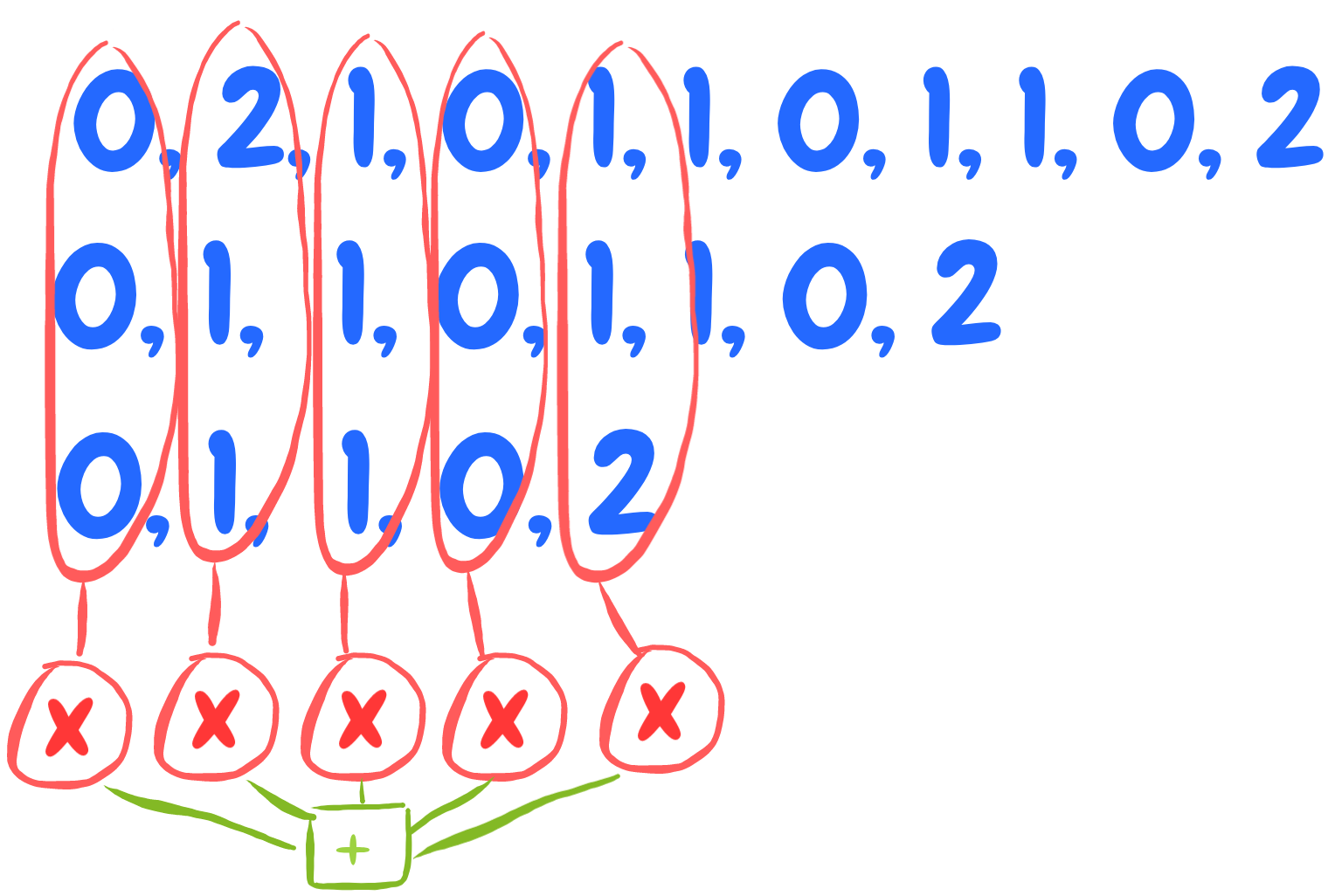
Here is an implementation in Python:

1
2
3
4
5
6
7
8

def beautifulTriplets(d, a):
    f=[0]*(2*10000+1)
    for i in a:
        f[i]=f[i]+1
   
    z = zip(f, f[d:], f[d+d:])
    mapped = map(lambda t : reduce(operator.mul, t, 1), z);
    return sum(mapped)

Here is a possible implementation of the solution above with C++20 ranges:

1
2
3
4
5
6
7
8

vector<int> f(2*10000+1);
for (auto i : a)
    f[i]++;

auto z = view::zip(f, view::drop(f, d), view::drop(f, d+d));
auto mapped = view::transform(z, [](const auto& t) { 
    return get<0>(t)*get<1>(t)*get<2>(t); } );
cout << ranges::accumulate(mapped, 0);

Exploting some metaprogramming, we can generalise the calleble into transform:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

template <size_t index, class Op, typename... Ts>
constexpr auto tuple_fold(Op op, const std::tuple<Ts...>& t) 
{
    if constexpr(index == sizeof...(Ts) - 1) 
    {
        return std::get<index>(t);
    } 
    else 
    {
        return op(std::get<index>(t), tuple_fold<1 + index>(op, t));
    }
}

struct mul_tuple
{
    template <typename ... Ts>
    constexpr auto operator()(const std::tuple<Ts...>& t1)  
    {
        return tuple_fold<0>(std::multiplies<>{}, t1);
    }    
};

// same as before except for:
auto mapped = view::transform(z, mul_tuple{});

Benchmark

See here a quick benchmark of some of the previous solutions (the domain is a bit different).

Try increasing \( d \) and see how LinearDSmall gets worse.