Find Kth Zero · Coding Gym

Consider an array of integers A = [a1, a2, …, aN]. We can perform two types of queries on A:

1 k: For query type 1, find and print an integer denoting the index of the kth zero in array A on a new line; if no such index exists (i.e., there is no zero), print NO instead.
p x: For query type 2, replace the element positioned at index p with integer x (i.e., set A[p] = x).

Given A’s initial state and queries, perform each query in order. For each query of type 1, print the query’s answer on a new line.

Input Format

The first line contains two space-separated integers describing the respective values of n (the size of the array) and m (the number of queries). he second line contains space-separated integers describing the respective elements of array A (e.g. a0, a1, …, aN).

Each of the m subsequent lines describes a query in one of the following forms:

1 k, where 1 is the query type and k denotes the kth zero you must locate an index for in the array.
2 p x, where 2 is the query type, p is the index (position) you must update, and x denotes the new value to store at A[p].

Constraints

1
2
3


0<= A[i], x<= 10'000
1<= n,k,m <= 10'000
0<= p < n

Output Format

For each query of type 1, print a single integer on a new line denoting the index where the kth zero is located in A; if no such index exists (i.e., there is no zero), print NO instead.

Solutions

Naïve solution

The naïve solution is to create the array just as it defined and do a linear search for each query.

Although update is fast (\( O(1) \)), the search is slow, because we need to search linearly the kth zero (\( O(N) \)).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


#include <iostream>
#include <vector>

int main() {
  std::string line;
  int n, m;
  std::cin >> n;
  std::cin >> m;

  std::vector<int> arr;

  while (n--) {
    int tmp;
    std::cin >> tmp;
    arr.push_back(tmp);
  }

  while (m--) {
    int queryType;
    std::cin >> queryType;
    if (queryType == 1) {
      int k;
      std::cin >> k;
      int found = 0;
      int i = 0;
      for (; i != arr.size(); ++i) {
        found += arr[i] ? 0 : 1;
        if (found == k) {
          break;
        }
      }

      if (found == k) {
        std::cout << i;
      } else {
        std::cout << "NO";
      }

      std::cout << "\n";

    } else if (queryType == 2) {
      int p, x;
      std::cin >> p;
      std::cin >> x;
      arr[p] = x;
    }
  }
}

Segment tree

In this Problem, we have two types of queries that are to be performed on the array. One is called as Kth Zero over a range and other is a Point update Query. For this class of problems, the suitable data structure is a Segment Tree.

Thus, the quickest solution uses such a data structure (credits to HackerRank):

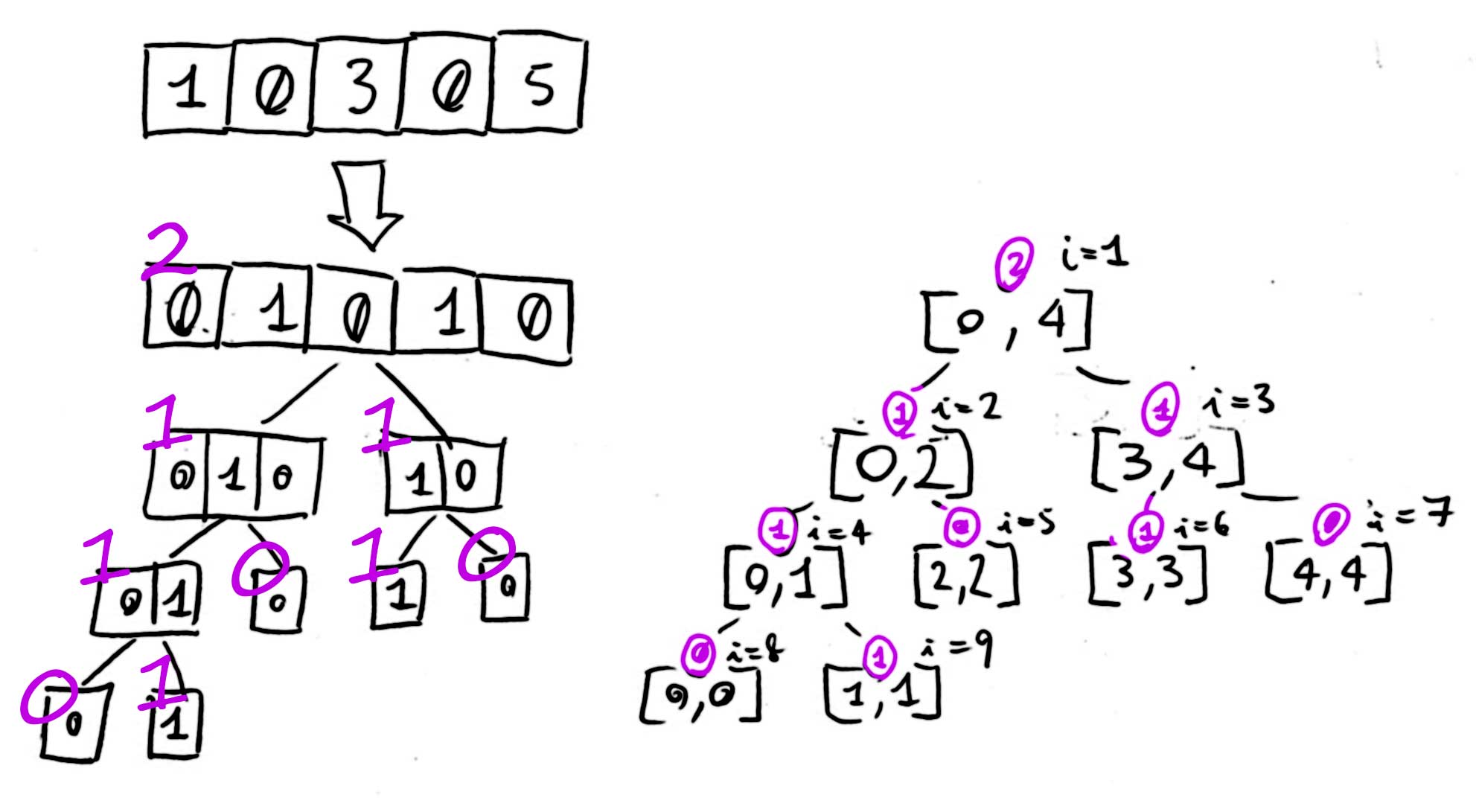
Build the tree. Node value is the count of zeroes in the range.

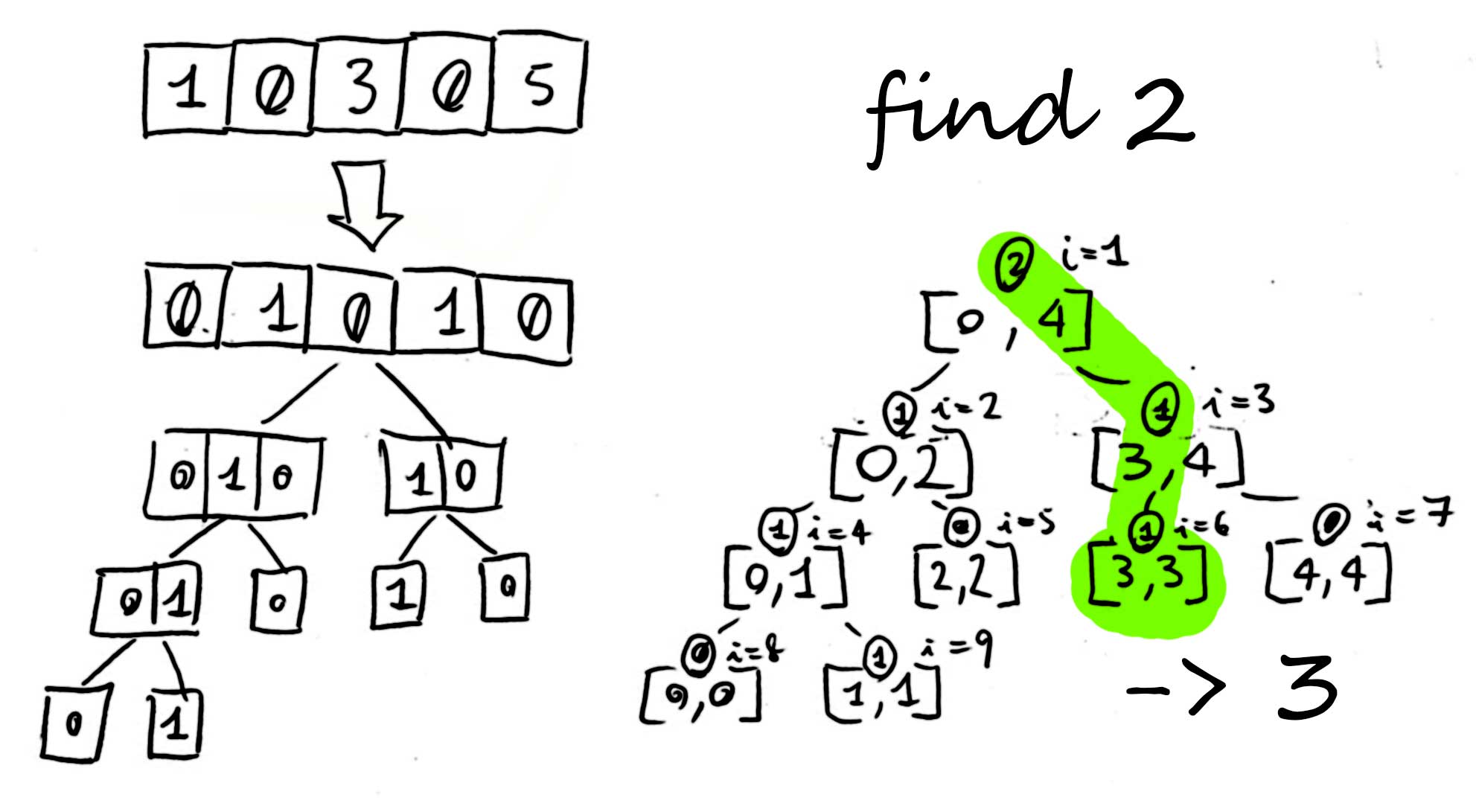
find kth zero

Find 2nd zero

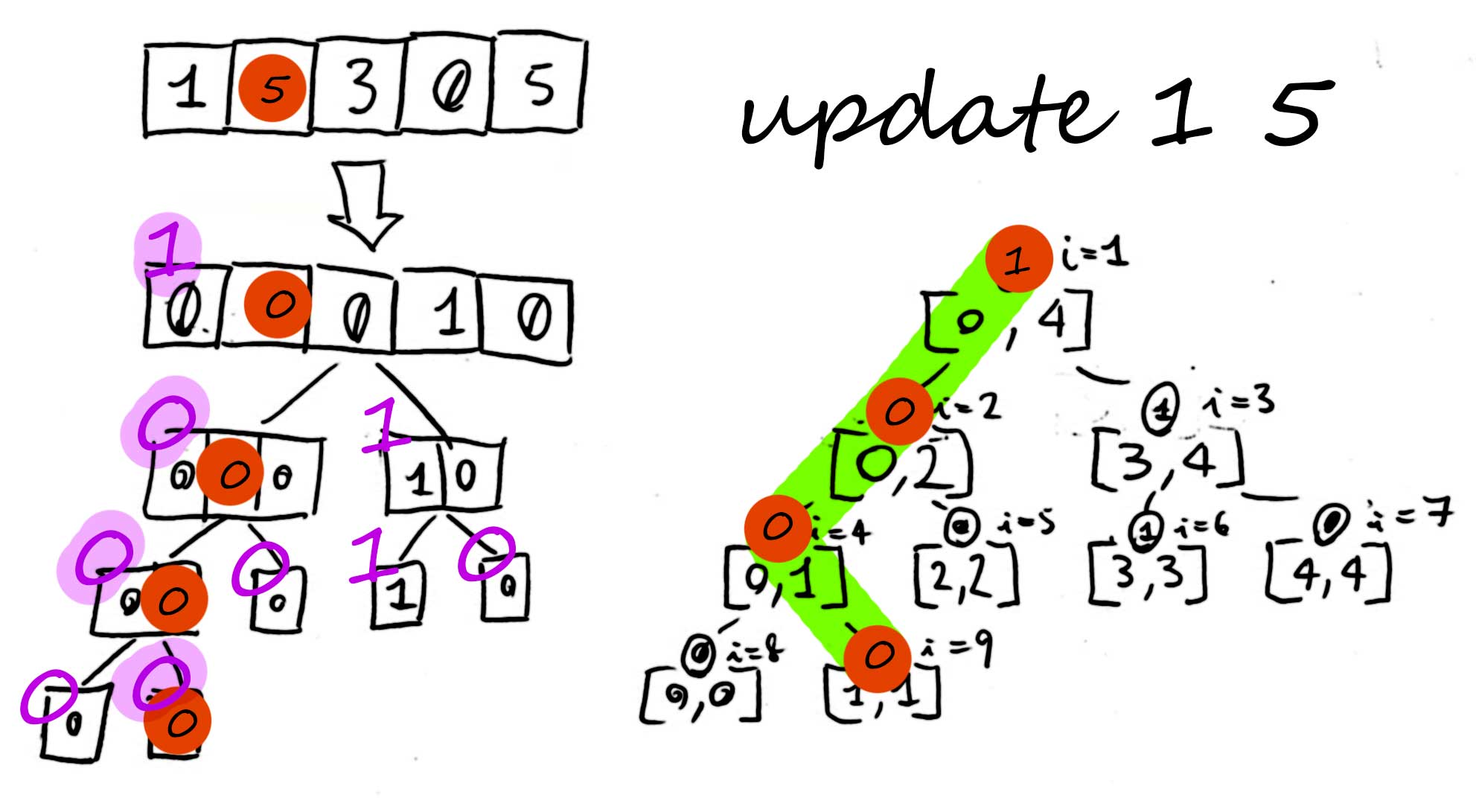
find kth zero

Change value at position 1 to 5

find kth zero

More info about segment trees:

Segment tree (C)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78


#include <stdio.h>

void buildTree(int tree[], int array[], int index, int low, int high) {
  if (low == high) {
    if (array[low] == 0) {
      tree[index] = 1;
    } else {
      tree[index] = 0;
    }
  } else {
    int mid = (low + high) / 2;
    buildTree(tree, array, index * 2, low, mid);
    buildTree(tree, array, index * 2 + 1, mid + 1, high);
    tree[index] = tree[index * 2] + tree[index * 2 + 1];
  }
}

void updateTree(int tree[], int index, int low, int high, int pos, int new_val) {
  if (low == high) {
    if (new_val == 0) {
      tree[index] = 1;
    } else {
      tree[index] = 0;
    }
  } else {
    int mid = (low + high) / 2;
    if (pos <= mid) {
      updateTree(tree, index * 2, low, mid, pos, new_val);
    } else {
      updateTree(tree, index * 2 + 1, mid + 1, high, pos, new_val);
    }
    tree[index] = tree[index * 2] + tree[index * 2 + 1];
  }
}

int find_kth(int tree[], int index, int low, int high, int k) {
  if (tree[index] < k) {
    return -1;
  }
  if (low == high) {
    return low;
  }
  int mid = (low + high) / 2;
  if (tree[index * 2] >= k) {
    return find_kth(tree, index * 2, low, mid, k);
  } else {
    return find_kth(tree, index * 2 + 1, mid + 1, high, k - tree[index * 2]);
  }
}

int main() {
  int n, m;
  scanf("%d%d", &n, &m);
  int arr[n], tree[4 * n + 1];
  for (int i = 0; i < n; i++) {
    scanf("%d", &arr[i]);
  }
  buildTree(tree, arr, 1, 0, n - 1);
  for (int i = 0; i < m; i++) {
    int type, k, pos, val;
    scanf("%d", &type);
    if (type == 1) {
      scanf("%d", &k);
      int ans = find_kth(tree, 1, 0, n - 1, k);
      if (ans == -1) {
        printf("NO\n");
      } else {
        printf("%d\n", ans);
      }
    } else {
      scanf("%d%d", &pos, &val);
      if (pos < n) {
        updateTree(tree, 1, 0, n - 1, pos, val);
      }
    }
  }
  return 0;
}

Segment tree (C++)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86


#include <iostream>
#include <vector>

void update_leaf(std::vector<int>& tree, int index, bool isZero) {
  tree[index] = isZero ? 1 : 0;
}

void update_node(std::vector<int>& tree, int index) {
  tree[index] = tree[index * 2] + tree[index * 2 + 1];
}

void build_tree(std::vector<int>& tree, const std::vector<bool>& arr, int index, int low, int high) {
  if (low == high) return update_leaf(tree, index, arr[low]);

  const int mid = (low + high) / 2;

  build_tree(tree, arr, index * 2, low, mid);
  build_tree(tree, arr, index * 2 + 1, mid + 1, high);
  update_node(tree, index);
}

void update_tree(std::vector<int>& tree, int index, int low, int high, int pos, bool isZero) {
  if (low == high) return update_leaf(tree, index, isZero);

  const int mid = (low + high) / 2;
  const bool goLeft = pos <= mid;
  const int nextIndex = index * 2 + (goLeft ? 0 : 1);
  const int nextLow = goLeft ? low : mid + 1;
  const int nextHigh = goLeft ? mid : high;

  update_tree(tree, nextIndex, nextLow, nextHigh, pos, isZero);
  update_node(tree, index);
}

int find_kth(const std::vector<int>& tree, int index, int low, int high, int k) {
  /* If in this branch there are less than k zeros, abort searching */
  if (tree[index] < k) return -1;

  /* If in a leaf, we've found it! */
  if (low == high) return low;

  /* Search in subtree */
  const int mid = (low + high) / 2;
  const bool goLeft = tree[index * 2] >= k;
  const int nextIndex = index * 2 + (goLeft ? 0 : 1);
  const int nextLow = goLeft ? low : mid + 1;
  const int nextHigh = goLeft ? mid : high;
  const int nextK = goLeft ? k : (k - tree[index * 2]);

  return find_kth(tree, nextIndex, nextLow, nextHigh, nextK);
}

int main() {
  int n, m;
  std::cin >> n >> m;

  std::vector<bool> arr;
  std::vector<int> tree(4 * n + 1);

  for (int i = 0; i != n; ++i) {
    int x;
    std::cin >> x;
    arr.push_back(x == 0);
  }

  build_tree(tree, arr, 1, 0, n - 1);

  while (m--) {
    int type, k, pos, val;
    std::cin >> type;

    if (type == 1) {
      std::cin >> k;
      int ans = find_kth(tree, 1, 0, n - 1, k);
      if (ans == -1) {
        std::cout << "NO\n";
      } else {
        std::cout << ans << "\n";
      }
    } else {
      std::cin >> pos >> val;
      update_tree(tree, 1, 0, n - 1, pos, val == 0);
    }
  }
  return 0;
}

Collection of zero’s indexes

However, the space cost is 4-times the problem dimension. A possible solution which allocates at most N elements but is ~4-times slower than the previous one consists in keeping track only of the zeros updates:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


#include <iterator>
#include <cstdio>
#include <deque>
#include <iostream>
#include <algorithm>
using namespace std;

int main()
{
    int n, m, elem; cin >> n >> m;
    deque<int> zeros;
    for (auto i=0; i<n; ++i)
    {
        cin >> elem;
        if (elem == 0)
            zeros.push_back(i);
    }
    int cmd, a1, a2;
    while (m--)
    {
        cin >> cmd;
        switch(cmd)
        {
        case 1:
            cin >> a1; --a1;
            cout << (a1>=zeros.size() ? "NO" : to_string(zeros[a1])) << "\n";
            break;
        case 2:
            cin >> a1 >> a2;
            auto it = lower_bound(begin(zeros), end(zeros), a1);
            if (it != end(zeros) && *it == a1 && a2!=0)
            {
                zeros.erase(it);
            }
            else if (a2 == 0)
            {
                zeros.insert(it, a1);
            }
            break;
        }
    }
}

Note: we used a std::deque that is, basically, a paged array. Replacing it with a std::vector is twice as slower.

Same algorithm but in Rust courtesy of Alessandro and Edoardo:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58


fn main() {
    use std::collections::BTreeSet;
    use std::io::{self, BufRead};

    let stdin = io::stdin();
    let handle = stdin.lock();

    let mut lines = handle
        .lines()
        .skip(1)
        .map(Result::unwrap)
        .map(|s| s.trim().to_string());
    let mut zero_positions: BTreeSet<_> = lines
        .next()
        .unwrap()
        .split(' ')
        .enumerate()
        .filter(|&(_, s)| s == "0")
        .map(|(index, _)| index)
        .collect();

    lines.for_each(|line| {
        let mut splitted = line.split(' ');
        match splitted.next().unwrap() {
            "1" => {
                let index = splitted
                    .next()
                    .unwrap()
                    .parse::<usize>()
                    .unwrap()
                    - 1usize;
                match zero_positions.iter().nth(index) {
                    Some(pos) => println!("{}", pos),
                    None => println!("NO"),
                }
            }
            "2" => {
                let index: usize = splitted
                    .next()
                    .unwrap()
                    .parse()
                    .unwrap();
                let value: u32 = splitted
                    .next()
                    .unwrap()
                    .parse()
                    .unwrap();

                if value == 0 {
                    zero_positions.insert(index);
                } else {
                    zero_positions.remove(&index);
                }
            }
            _ => unreachable!(),
        }
    })
}

binary search