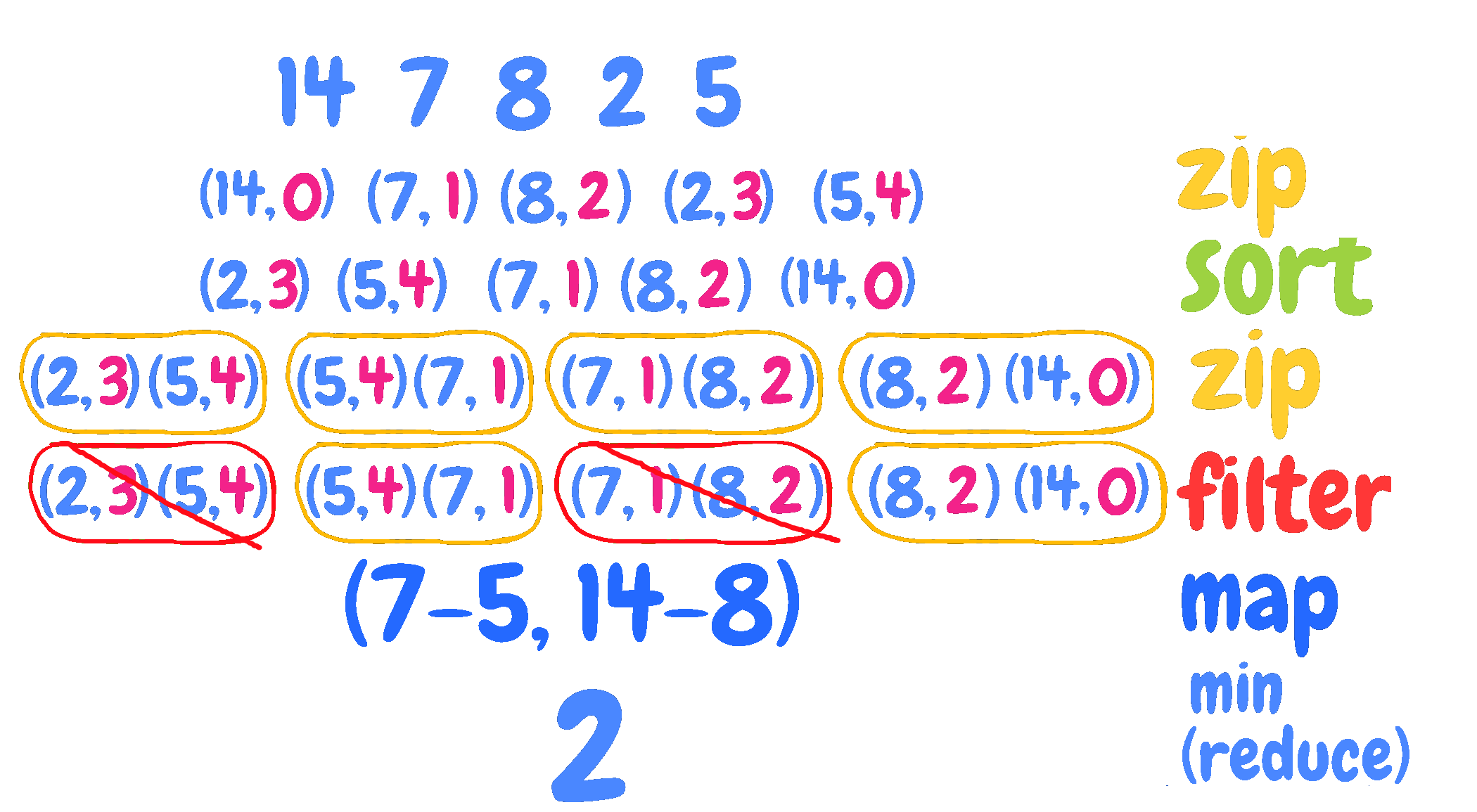See the original problem on HackerRank.
Solutions
The naive solution is quadratic and it’s too slow for a few test cases. We show it here, for completeness:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
#include <iterator>
#include <climits>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
vector<int> v(n);
copy_n(istream_iterator<int>(cin), n, begin(v));
auto minLoss = INT_MAX;
for (auto i=0; i<n; ++i)
{
for (auto j=i+1; j<n; ++j)
{
if (v[i] > v[j])
{
minLoss = min(minLoss, v[i] - v[j]);
}
}
}
cout << minLoss;
}
|
Rust naive solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
fn minimum_loss(prices: Vec<u64>) -> u64 {
let mut min_loss = std::u64::MAX;
for i in prices.iter() {
for j in prices.iter().skip(1) {
if i > j {
min_loss = min(min_loss, i - j);
}
}
}
min_loss
}
|
Set-based solution
We need to amortize the internal loop.
Suppose we process the elements in an online fashion (e.g. in streaming). The elements already processed constitute the “history” of our data. For the next element \(p\), we need to search the “history” for the first element greater than \(p\).
If our history is sorted, we can easily answer to the query with a binary search (or such). This is known as lower bound.
Thus, we can use a sorted data structure supporting such an operation.
In C++ we can use a std::set:
1
2
3
4
5
6
7
8
9
10
11
|
int N; cin >> N;
price i, loss = numeric_limits<price>::max();
set<price> prices;
while (cin >> i)
{
const auto lb = prices.lower_bound(i); // 👈💣
prices.insert(lb, i);
if (lb != end(prices))
loss = min(loss, *lb-i);
}
cout << loss;
|
In Java we can use a TreeSet:
1
2
3
4
5
6
7
8
9
10
11
12
13
|
Scanner in = new Scanner(System.in);
TreeSet<Integer> prices = new TreeSet<Integer>();
int loss = Integer.MAX_VALUE;
while (in.hasNext())
{
int elem = in.nextLong();
Integer ub = prices.higher(elem); // 👈💣
if (ub != null)
loss = Math.min(loss, ub-elem);
prices.add(elem);
}
System.out.println(loss);
in.close();
|
In Rust we can use a BTreeSet:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
fn minimum_loss<T: Iterator<Item = u64>>(prices: T) -> u64 {
let mut set = BTreeSet::new();
let mut min_loss = std::u64::MAX;
for price in prices {
let lb = set.range(price..).next().cloned();
set.insert(price);
if let Some(lb) = lb {
min_loss = min(min_loss, lb - price);
}
}
min_loss
}
|
In C# we can use SortedSet, left as an exercise.
The cost of this solution is \(O(N \cdot logN) \).
What happens if duplicates kick in and 0 is not admitted as minimum loss?
We should replace lower bound with upper bound, to skip the duplicates.
Sort-based solution
Even more efficient is to preprocess data.
Intuition: if the prices are sorted, the minimum loss is given by two adjacent prices. We just need to check if the pair is “valid”, that is: if the sell price is actually following the purchase (the sell is in the future).
Thus, we can duplicate our data and add an index for each price. The index is ascending and it just represents then history.
For example, for: 14 7 8 2 5
We have:
(0, 14) (1, 7) (2, 8) (3, 2) (4, 5)
Now we can sort the data and the history won’t be lost:
(3, 2) (4, 5) (1, 7) (2, 8) (0, 14)
We can finally process adjacent pairs. Since we sell at a loss:
- the right pair (price is bigger) represents the purchase price
- the left pair (price is lower) represents the sell price
We only need to wipe out pairs that are not admittable, that is purchase happens
after the sell.
For example, (3, 2) and (4, 5) must be discarded because purchase (4, 5)
happens after the sell (3, 2), since the position 4 is greater than the position 3.
On the other hand, (4, 5) and (1, 7) are ok because (1, 7) is before (4, 5).
A possible C++ implementation follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
int main()
{
int n; cin >> n;
vector<pair<long long, int>> v(n);
int idx = 0;
// map values to (idx, value)
transform(
istream_iterator<long long>(cin),
istream_iterator<long long>(),
begin(v),
[&](auto i){return make_pair(i, idx++);}
);
sort(begin(v), end(v));
auto minLoss = numeric_limits<long long>::max();
for (auto i=1; i<n; ++i)
{
if (v[i].second < v[i-1].second)
{
minLoss = min(v[i].first-v[i-1].first, minLoss);
}
}
cout << minLoss;
}
|
The solution above is just an application of three patterns: zip | map | reduce.
A picture worth a thousand words:
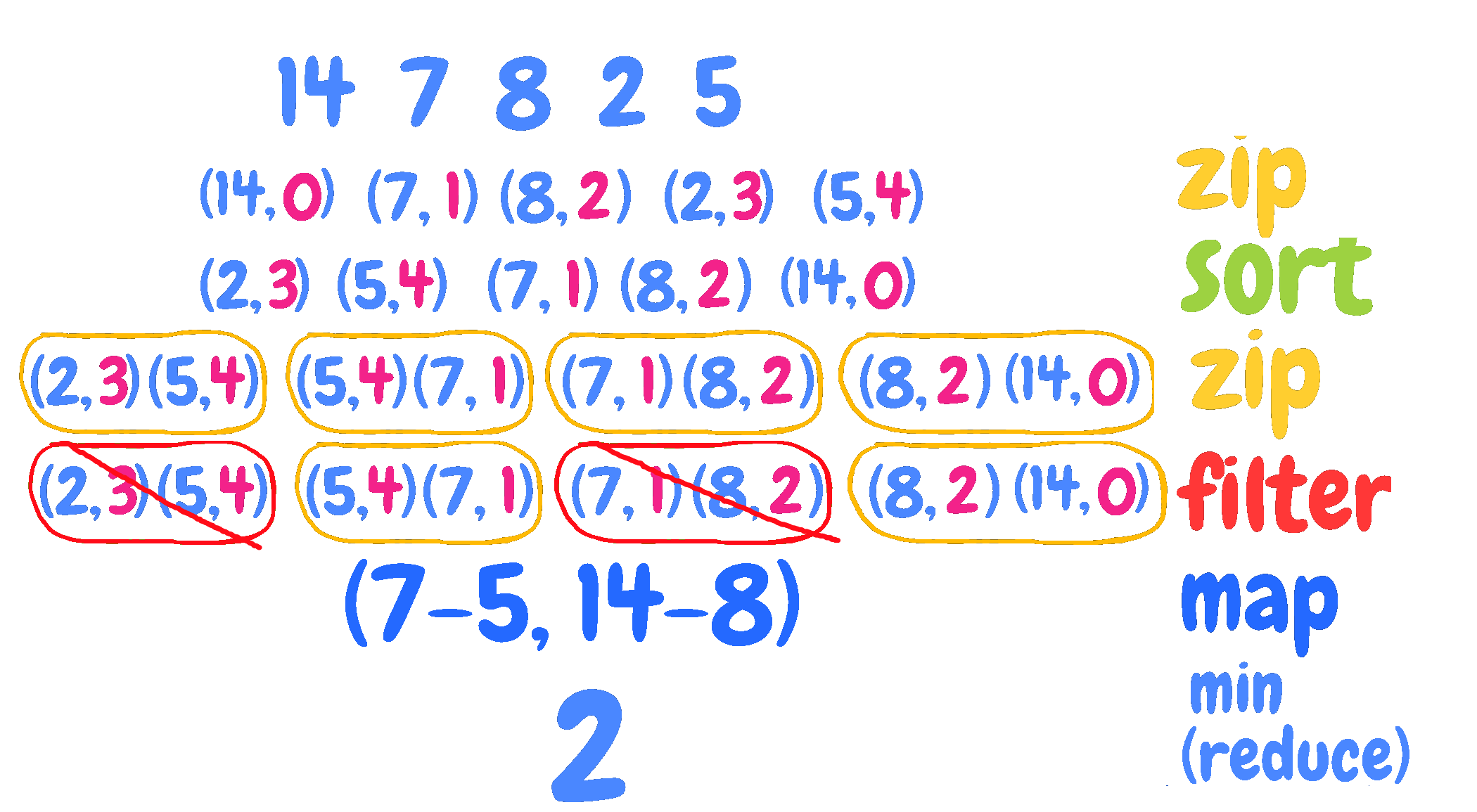
In C++ this can be implemented in terms of std::inner_product:
1
2
3
4
5
6
7
8
|
cout << inner_product(next(begin(v)), end(v), begin(v),
numeric_limits<long long>::max(),
[](auto... m) { return min(m...); },
[](const auto& p1, const auto& p2) {
return p1.second < p2.second ?
p1.first-p2.first :
numeric_limits<long long>::max();
});
|
That is not straightforward.
Here is an experimental version that makes extensive use of C++20 ranges:
1
2
3
4
5
6
7
8
|
auto pairs = views::zip(v, views::ints(0, (int)v.size()))
| ranges::to<std::vector<std::pair<int, int>>>()
| actions::sort;
std::cout << ranges::min(
views::zip(pairs, views::drop(pairs, 1))
| views::remove_if([](const auto& pack) { return pack.first.second < pack.second.second;})
| views::transform([](const auto& pack) { return pack.second.first - pack.first.first; }));
|
views::zip(v, views::ints(0, (int)v.size())) creates pairs of values with their position. views::enumerate is similar except for the order of the pairs.
The second code block is a bit confusing because of the second application of zip that makes the range more convoluted. If you find any better ways, please comment this post!
Python is a valuable ally:
1
2
3
4
5
6
7
|
index = range(0, len(price))
zipped = zip(price, index)
zipped.sort(key = lambda t: t[0])
zipped = izip(zipped, zipped[1::])
valids = ifilter(lambda (x1, x2): x1[1]>x2[1], zipped)
differences = imap(lambda (x1, x2) : x2[0]-x1[0], valids)
print min(differences)
|
Or, more pythonic:
1
2
3
4
5
6
|
index = range(len(price))
zipped = sorted(zip(price, index), key=lambda x: x[0])
zipped = zip(zipped, zipped[1::])
valids = ((x1, x2) for x1, x2 in zipped if x1[1] > x2[1])
differences = (x2[0] - x1[0] for x1, x2 in valids)
print min(differences)
|
Haskell:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
import Data.List (sortBy)
comparePrices (a,_) (b,_) = compare a b
validPair ((_, sell), (_, buy)) = buy < sell
loss ((sellPrice, _), (buyPrice, _)) = buyPrice - sellPrice
main = do
_ <- getLine
pricesStr <- getLine
let prices = read <$> words pricesStr :: [Int]
let pricesAndIndexes = zip prices [0..]
let sortedByPrice = sortBy comparePrices $ pricesAndIndexes
let valids = filter validPair $ zip sortedByPrice (tail sortedByPrice)
let differences = loss <$> valids
print $ minimum differences
|
Another haskell version, using list comprehension:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
import Control.Monad (ap)
import Data.List (sortOn)
minimumLoss xs =
minimum
[ bPrice - sPrice
| ((sPrice, _), (bPrice, _)) <-
[ x
| x@((_, s), (_, b)) <- ap zip tail $ sortOn fst $ zip xs [0 ..]
, b < s
]
]
main = interact (show . minimumLoss . fmap read . tail . words)
|
This solution is faster than the set-based one. Possible cons are:
- it does not work online (it requires preprocessing)
- it requires some extra memory to store the indices
A functional solution in Scala:
1
2
3
4
5
6
7
|
def minimumLoss(price: List[Long]): Long = {
val priceIndexed = price.zip(price.indices).sortWith(_._1 < _._1)
val pairs = priceIndexed.zip(priceIndexed.tail)
val validPairs = pairs.filter(p => p._1._2 > p._2._2)
val losses = validPairs.map(p => p._2._1 - p._1._1)
losses.min
}
|
A functional solution in Rust. The input is parsed directly to the vector,
avoiding a copy of the line in memory.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
use std::error::Error;
use std::io::BufRead;
use std::iter::FromIterator;
fn minimum_loss<T>(prices: T) -> u64
where
T: std::iter::Iterator<Item = u64>,
{
/* Here `prices` becames a Vec of (time, price) */
let mut prices = Vec::from_iter(prices.enumerate());
/* It is sorted in place (no memory is allocated */
prices.sort_by(|(_, a), (_, b)| a.cmp(b));
/* The actual iteration starts only when `min()` is called */
prices
.iter()
.zip(prices.iter().skip(1))
.filter(|((sell_time, _), (buy_time, _))| buy_time < sell_time)
.map(|(&(_, sell_price), &(_, buy_price))| buy_price - sell_price)
.min()
.unwrap()
}
fn main() -> Result<(), Box<dyn Error>> {
let stdin = std::io::stdin();
let line = stdin
.lock()
.lines()
.skip(1)
.next()
.ok_or("Missing line")??;
let prices = line.split_whitespace().flat_map(str::parse);
/* `prices` is just an iterator, parsing is not done yet */
let result = minimum_loss(prices);
println!("{}", result);
Ok(())
}
|
The solution doesn’t need a stable algorithm, and Rust let choose other
sorting algorithms. This should be faster than a simple sort_by.
1
|
prices.sort_unstable_by_key(|&(_, price)| price);
|