Product of Array Except Self

See the original problem on HackerRank.

Given an array of $ n $ integers where $ n > 1 $, $ nums $, print an array $ output $ such that $ output[i] $ is equal to the product of all the elements of $ nums $ except $ nums[i] $.

Solve the problem in $ O(N) $ without using division.

Input Format

Integer $ n $ denoting the number of elements followed by $ n $ space-separated integers - $ nums $. $ 0 < nums[i] < 20 $

Constraints

$ i < n < 10 $

Output Format

$ n $ integers (an array $ output $ such that each $ output[i] $ is equal to the product of all the elements of except $ nums[i] $).

Sample Input

Sample Output

1

120 60 40 30 24

Solutions

This problem is interesting because of two constraints:

Linear time complexity
No division can be used

We can solve this problem in two linear steps, by using an additional vector (the red one, in the following figure):

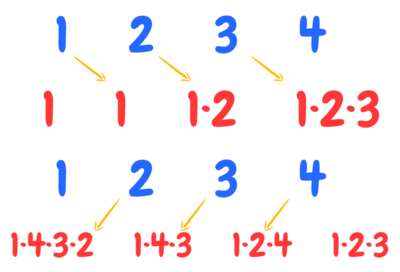
The idea is to keep a “prefix product” from the first element of the input vector, starting writing at the second position of the support vector. Then we do the same in the opposite way.

Here is the code. partial_sum is a C++ function performing a prefix-sum-like scan, open to any “sum” operation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


int n; cin >> n;
vector<long long> v(n);
copy_n(istream_iterator<long long>(cin), n, begin(v));
vector<long long> out(n, 1);
partial_sum(begin(v), end(v)-1, begin(out)+1, multiplies<>{});

auto curr = v.back();
for (auto i = 2; i <= v.size(); ++i)
{
    out[v.size() - i] *= curr;
    curr *= v[v.size() - i];
}

copy(begin(out), end(out), ostream_iterator<long long>(cout, " "));

To show the prefix-sum pattern, here is a very compact solution using another $O(N)$ support vector:

1
2
3
4
5
6
7


int n; cin >> n;
vector<long long> v(n);
copy_n(istream_iterator<long long>(cin), n, begin(v));
vector<long long> out1(n, 1), out2(n, 1);
partial_sum(begin(v), end(v)-1, begin(out1)+1, multiplies<>{});
partial_sum(rbegin(v), rend(v)-1, rbegin(out2)+1, multiplies<>{});
transform(begin(out1), end(out1), begin(out2), ostream_iterator<int>(cout, " "), multiplies<>{});

Rust solution, imperative style.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


fn product_of_array_except_self(arr: &[usize]) -> Vec<usize> {
    let mut res = vec![1; arr.len()];
    let mut acc = 1;
    for i in 0..(arr.len() - 1) {
        acc *= arr[i];
        res[i + 1] = acc;
    }
    let mut acc = 1;
    for i in (1..(arr.len())).rev() {
        acc *= arr[i];
        res[i - 1] *= acc;
    }
    res
}

Solution without extra space

We can use logarithm properties:

$ x = a \cdot b \cdot c $

$ Log(x) = Log(a \cdot b \cdot c) $

$ Log(x) = Log(a) + Log(b) + Log(c) = sum $

$ x = 10^{sum} $

$ \dfrac{x}{a} = 10^{sum - Log(a)} $

1
2
3
4
5
6


auto sum = accumulate(begin(v), end(v), 0.0L, [](auto sum, auto i){
    return sum+(long double)log10(i);
});

for (int i = 0; i < n; i++)
    cout << (int)(EPS + pow(10.00L, sum - log10(v[i]))) << " ";

Rounding can be an issue of this solution. It’s a compromise to take into account.

Credits of this solution: https://www.geeksforgeeks.org/product-array-puzzle-set-2-o1-space/

math constrained prefix sum