The Next Greater Element

See the original problem on HackerRank.

Given an array, print the Next Greater Element (NGE) for every element. The Next greater Element for an element \( x \) is the first greater element on the right side of \( x \) in array.

Elements for which no greater element exist, consider next greater element as \( -1 \).

Input Format

You are given \( N \), the number of elements, followed by \( N \) space-separated integer values.

Constraints

• \( 2 \leq N \leq 10^6 \)

Array values are 32bit integers.

Output Format

For each element of the array \( arr_i \) print its NGE, in the same order of the array.

Solutions

The naive solution consists in using two loops: for each element we find the next greater element. This solution is quadratic because for each element we pay a linear search.

The worst case is when the array is sorted in decreasing order.

Linear solution using stack

We could optimize by using a stack:

1. push the first element to the stack;
2. process the second element;
3. if the top of the stack is greater/equal than the current number then add that number to the stack;
4. if the top of the stack is less than the current number then keep on popping elements from the stack until the top of the stack is greater/equal to the current number OR the stack gets empty. The current number is the NGE of all the elements popped from the stack;
5. if the stack is not empty at the end of all iterations, mark the NGE of remaining items in stack as -1.

Here is an implementation in C++:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

int n; cin >> n;
vector<int> nums(n);
copy_n(istream_iterator<int>(cin), n, begin(nums));

unordered_map<int, int> nge;
std::stack<int> s;

for (auto i : nums)
{
    while (!s.empty() && s.top() < i)
    {
        nge[s.top()] = i;
        s.pop();
    }
    s.push(i);
}

for (auto i : nums)
{
    auto it = nge.find(i);
    cout << (it != end(nge) ? it->second : -1) << " ";
}

We put elements in a vector just for convenience - we could have processed elements straight from the input.

Since the output has to be in order, we need an additional data structure to maintain the results. We used a map but we can use a vector, getting very likely better performance.

Instead of using a dictionary (std::unordered_map in the example above), we can store result at the index. Just put in the stack the pair index/value as in the example below:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

std::vector<int> solve(const std::vector<int>& numbers) {
    const int n = numbers.size();
    std::vector<int> result(n, -1);
    std::stack<std::pair<int, int>> stack;

    for (int i = 0; i < n; ++i) {
        int x = numbers[i];

        while (!stack.empty()) {
            int top = stack.top().second;
            int j = stack.top().first;

            if (x > top) {
                result[j] = x;
                stack.pop();
            } else {
                break;
            }
        }

        stack.push(std::make_pair(i, x));
    }

    return result;
}

Variation: what if the array has duplicates? Although the core idea still holds, the way we store NGEs needs to be changed a bit.

Linear solution using an index array

Instead of storing NGEs, we can instead store their indices in a vector indices.

Here is the idea:

1. we iterate backwards from the second-last element (the last does not have NGE1). Say this is index i. Also, put j=i+1;
2. if nums[j] (the next one) is greater than nums[i], then nums[j] is nums[i]’s’ NGE;
3. if nums[j] (the next one) is less than nums[i], then we compare nums[i] with nums[indices[j]] - that is the NGE of nums[j]. Let’s update j=indices[j]
4. we repeat the previous step until we fall into step 2 or we find -1
5. indices contain all the indices of NGEs (or -1) for each number

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

int n; cin >> n;
vector<int> nums(n);
copy_n(istream_iterator<int>(cin), n, begin(nums));
   
vector<int> indices(nums.size(), -1);  

for (int i = nums.size() - 2; i >= 0; i--) 
{
  auto j = i + 1;
  while (j != -1 && nums[j] <= nums[i]) 
    j = indices[j];

  indices[i] = j;
}

for (auto i : indices)
{
    cout << (i==-1 ? -1 : nums[i]) << " ";
}

Basically, indices is used to “jump” through NGEs.

A visual example follows.

Suppose we have the input array: 10 3 6 5 20.

We initialize indices with -1:

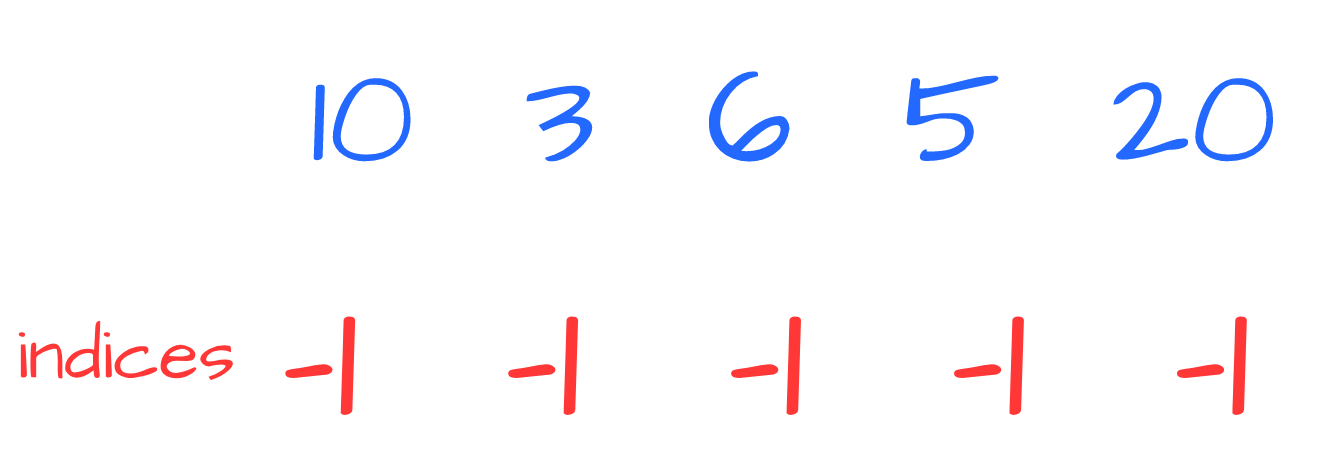
Starting from the end of the array, we process 5 and 20:

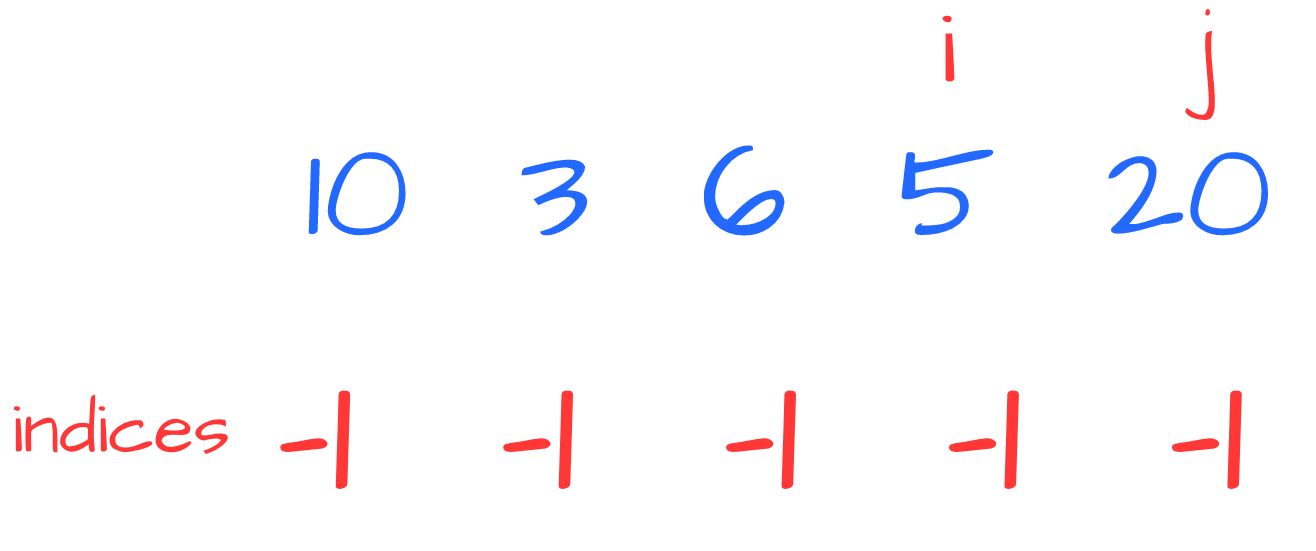
Since (( 5<20 )) we know that 20 is NGE of 5:

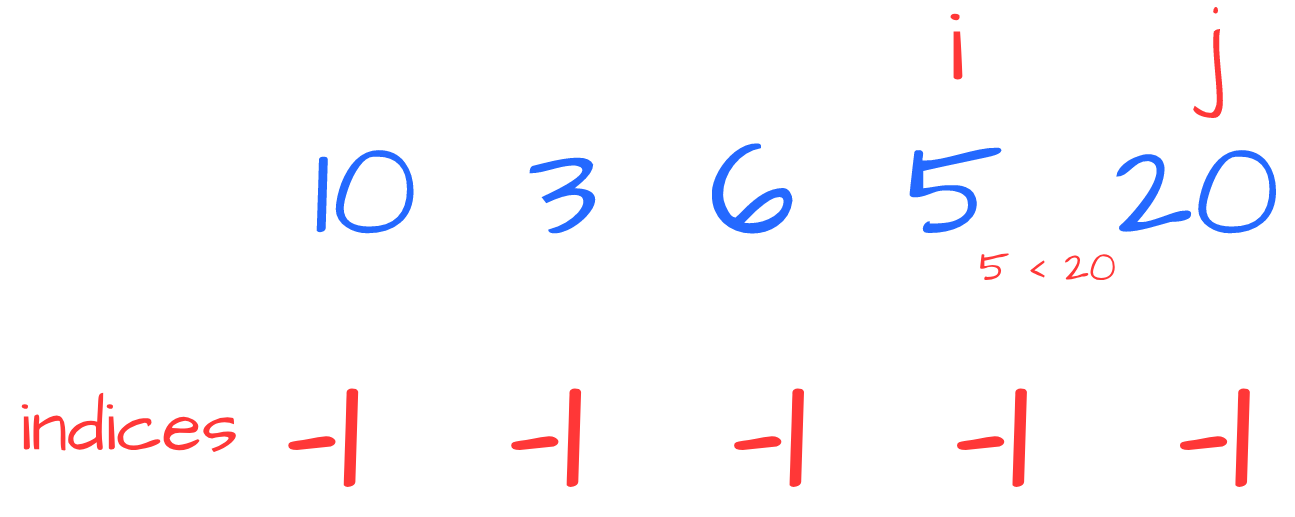
We update indices:

Then we process 6 and 5:

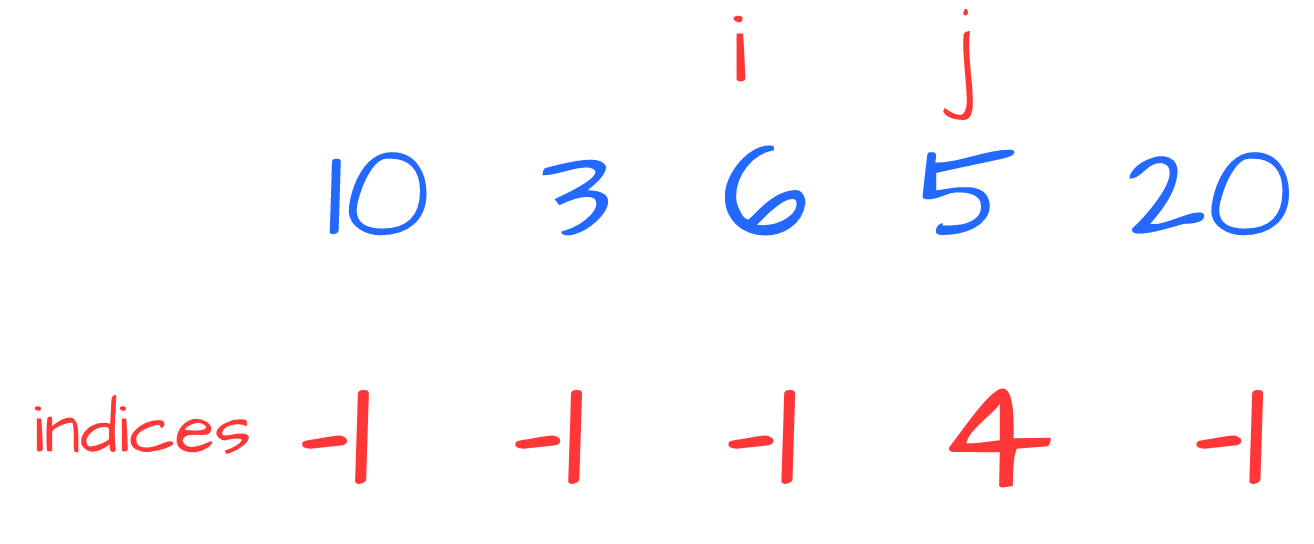
This time (( 6>5 )) then we use replace 5 with its NGE - 20:

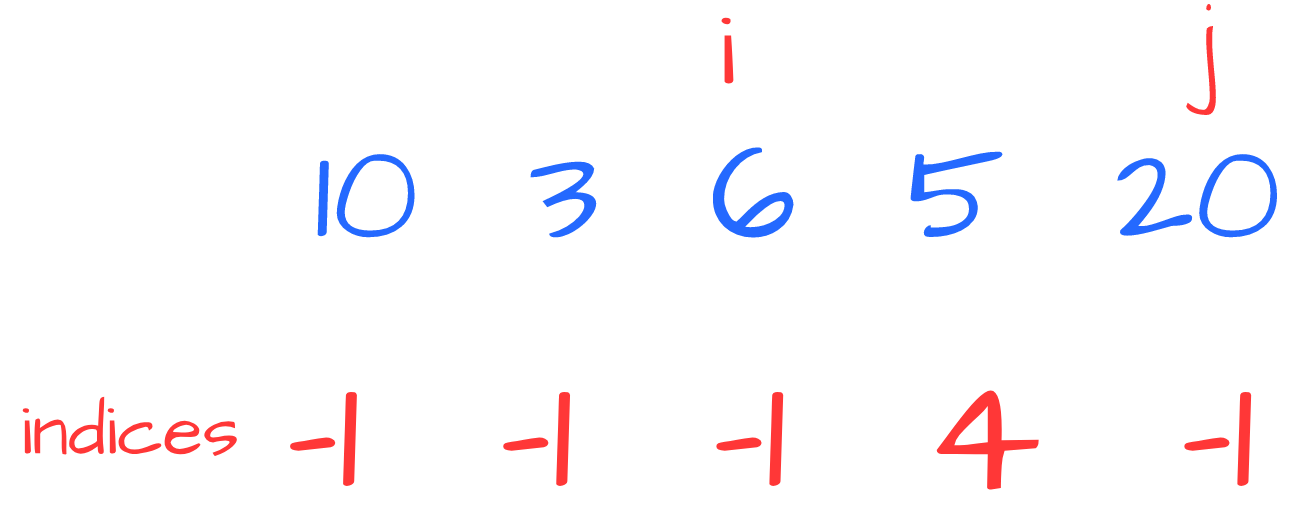
Such a value is greater than 6 thus we have found NGE for 6:

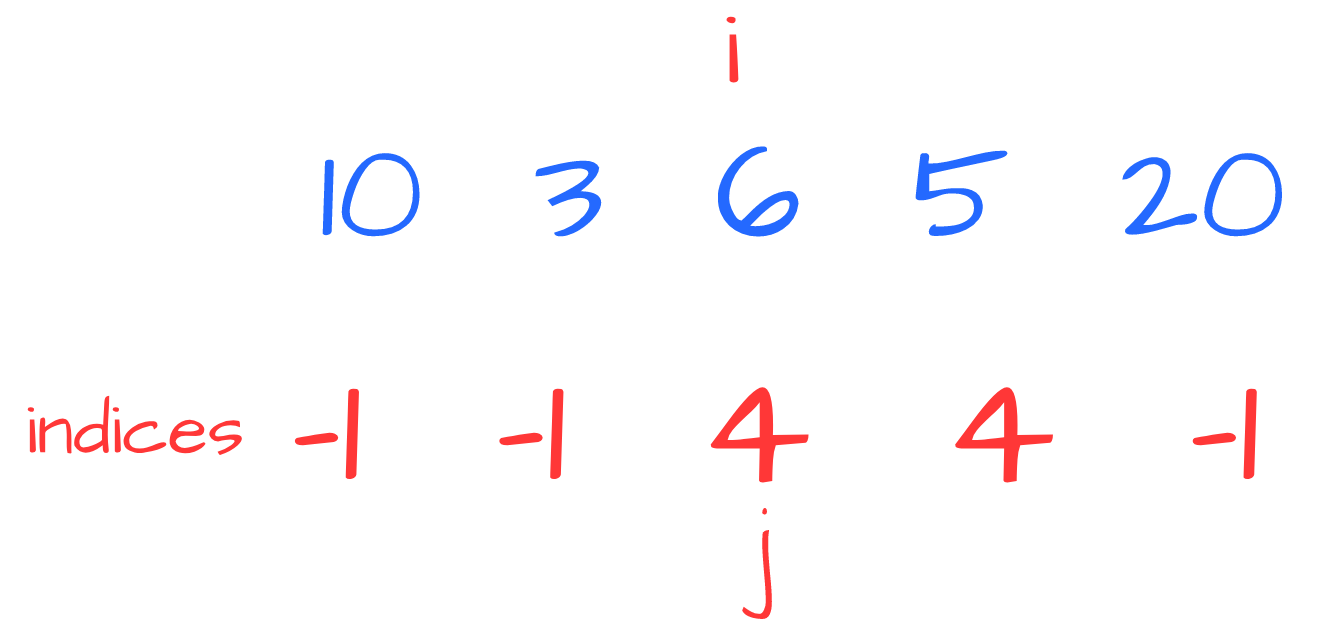
Now we have 10 and 3:

Since (( 10>3 )) we “jump” to 3’s NGE, that is 6. Again, (( 10>6 )) so we jump to 6’s NGE, that is 20:

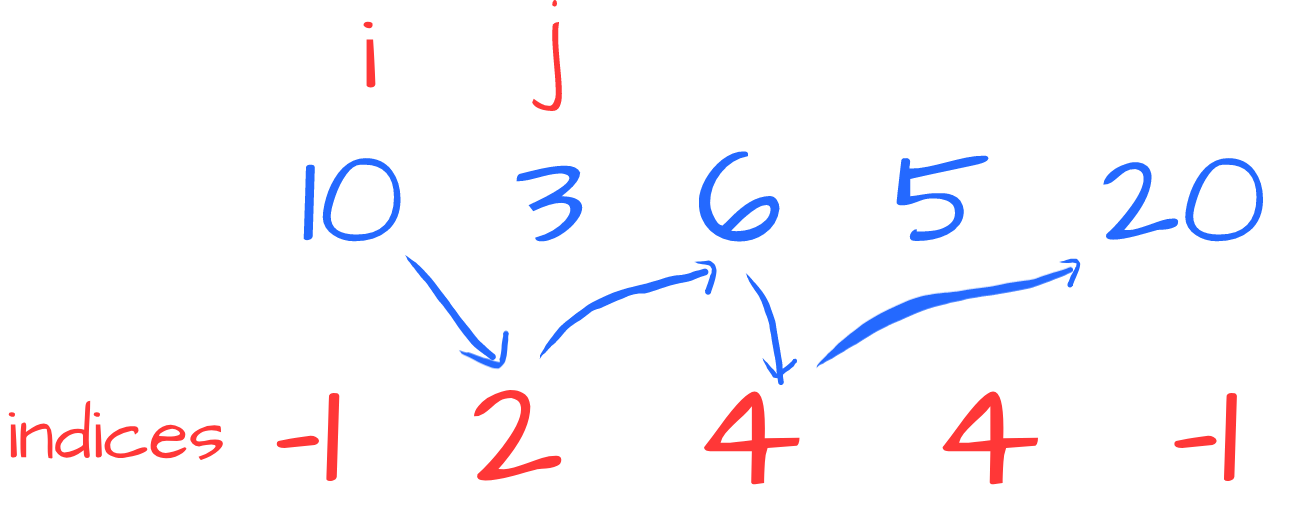
Since (( 20>10 )) we have found NGE for 10:

That’s it!

Although are both linear, this solution may be slightly faster than the previous one because the index array is contiguous and not dynamic. This could result in a better usage of the memory and the cache. In addition, we don’t need extra space to keep results in order.

If we vary the problem by introducing duplicates, this solution is already capable of handling the new requirement since indices (aka: NGE indices) is positional.