Triple Sum

See the original problem on HackerRank.

Solutions

Consider this test case:

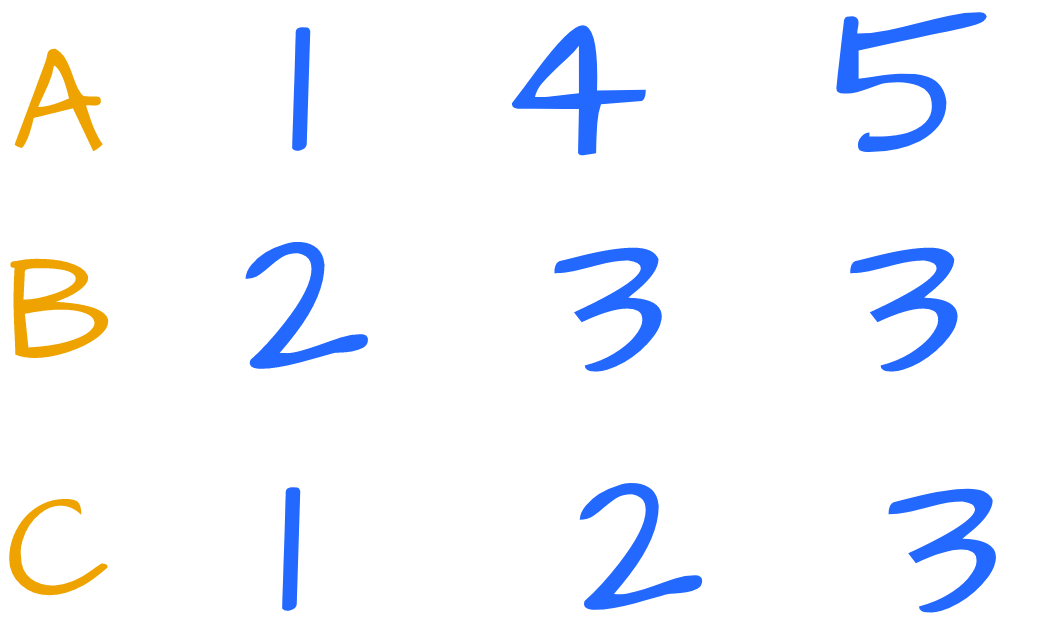
Visually, for each element of B we should mark the elements in A and C that are less than or equal to that element:

And, for 3:

Performing the operation on the second 3 is redundant, because triplets must be unique.

Along the way, we could multiply the count of A’s marked elements with the count of B’s marked elements. All the results will be then accumulated.

For B[0] (2) we have:

1
2
3

A = [1] (1 element)
C = [1, 2] (2 elements)
Partial: 1x2=2

For B[1] (3) we have:

1
2
3

A = [1] (1 element)
C = [1, 2, 3] (3 elements)
Partial: 1x3=3

Thus, the total is 2+3=5.

Clearly, solving the problem with a brute force approach is easy and \( O(N^2)\).

We can do better.

First of all, since triplets should be unique, we can remove all the duplicates from the arrays. Generally, we do it by sorting the arrays first.

To solve this problem, sorting is the key step.

Having the array sorted and without duplicates, we can think about an efficient approach. After all, for each element of B we need to find how many elements are smaller or equal in A and C.

Upper Bound

Given a sorted array and a value, we know how to efficiently find the span of elements smaller than such value: it’s a job for binary search and in particular for upper bound.

upper bound finds the first element strictly greater than the wanted value in logarithmic time. In our languages, upper bound (or whatever called) is generally implemented by returning a position (or iterator, index, etc).

For example, assuming 0-based indexing, if the upper bound of an element a is at position 2 then 2 elements appear before a (remember the array has no duplicates).

Thinking in C++ and Python, upper_bound and bisect return the first position after the wanted element. Thus, for each element bi of the array b we use upper_bound (or bisect) to find the right end (exclusive - as in C++ convention) of the span of elements less than or equal to bi. The size of such a span is the number of elements that we look for at each step.

Let’s dive into some coding. Here is a C++ solution:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

auto input(int len)
{
    vector<int> res(len);
    copy_n(istream_iterator<int>(cin), len, begin(res));
    sort(begin(res), end(res));
    res.erase(unique(begin(res), end(res)), end(res));
    return res;
}

int main()
{
    int la, lb, lc;
    cin >> la >> lb >> lc;
    auto a = input(la);
    auto b = input(lb);
    auto c = input(lc);

    unsigned long long count = 0ull;
    for (auto bi : b)
    {
        auto lba = upper_bound(begin(a), end(a), bi);
        auto lbc = upper_bound(begin(c), end(c), bi);
        unsigned long long cardA = distance(begin(a), lba);
        unsigned long long cardC = distance(begin(c), lbc);
        count += cardA * cardC;
    }
    
    cout << count;
}

The magic happens when we calculate the distance from the beginning, because in C++ we get an iterator back from upper_bound.

Looking carefully, there is a pattern emerging from the previous snippet. It’s a reduce (foldl, accumulate)!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

auto input(int len)
{
    vector<int> res(len);
    copy_n(istream_iterator<int>(cin), len, begin(res));
    sort(begin(res), end(res));
    res.erase(unique(begin(res), end(res)), end(res));
    return res;
}

int main()
{
    int la, lb, lc;
    cin >> la >> lb >> lc;
    auto a = input(la);
    auto b = input(lb);
    auto c = input(lc);

    cout << accumulate(begin(b), end(b), 0ull, [&](auto cnt, auto bi){
        return cnt + 
            distance(begin(a), upper_bound(begin(a), end(a), bi)) * 
            distance(begin(c), upper_bound(begin(c), end(c), bi));
    });
}

Note that 64bit ints are needed or we overflow (here we used unsigned long long because, for example, on Windows using just long is not enought since it is 32bit).

Here is a more succinct Python solution (just the core part):

1
2
3

def triplets(a, b, c):
    a, b, c = sorted(set(a)), sorted(set(b)), sorted(set(c))   
    return sum(bisect.bisect(a, x) * bisect.bisect(c, x) for x in b)

set automatically removes duplicates and sorted sorts the result. Finally, the results coming from the list comprehension are summed up.

This solution is \( O(N \cdot logN) \).

Simple optimization

If we go back to our first example, we note very clearly that when we iterate on B[i+1] (e.g. 3) we carry all the elements found for B[i] (e.g. 2). What if we start upper bound from the results of the previous?

Here is the idea (just the main part because the rest is unchanged):

1
2
3
4
5
6
7
8
9

auto lba=begin(a), lbc=begin(c); // maintain some state
for (auto bi : b)
{
    lba = upper_bound(lba, end(a), bi);
    lbc = upper_bound(lbc, end(c), bi);
    unsigned long long cardA = distance(begin(a), lba);
    unsigned long long cardC = distance(begin(c), lbc);
    count += cardA * cardC;
}

This solution is still \( O(N \cdot logN) \), although we ammortized the constant factor of the core algorithm since the span of binary search is decreased at every iteration.

Clearly, the tradeoff is that now the algorithm is stateful. If we want to massively parallelize it, we should use one of the other versions.

However, this optimization opens the doors to a better solution whose core part is linear.

Sort + simple loop

There is a better solution which visits elements only once, so it’s linear. Credits to Andrea Battistello, Simone Carani, Elia Giacobazzi and Roberto Melis who proposed similar solutions at Coding Gym Modena in December 2018.

Conceptually, starting from the previous solution, just replace upper_bound with find_if - whose predicate is just element > bi.

In other words, we find the positions of first elements greater than bi in both a and c, and we keep track of such positions (iterators, indexes) to start from there afterwards.

This way, each element is visited only once and the core part is linear (overall is still \( O(N \cdot logN) \)).

Here is our C++ adaptation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

using namespace std;

auto input(int len)
{
    vector<int> res(len);
    copy_n(istream_iterator<int>(cin), len, begin(res));
    sort(begin(res), end(res));
    res.erase(unique(begin(res), end(res)), end(res));
    return res;
}

int main()
{
    int la, lb, lc;
    cin >> la >> lb >> lc;
    auto a = input(la);
    auto b = input(lb);
    auto c = input(lc);

    unsigned long long count = 0ull;
    auto lba = begin(a), lbc = begin(c);
    for (auto bi : b)
    {
        lba = find_if(lba, end(a), [=](auto v){ return v>bi; });
        lbc = find_if(lbc, end(c), [=](auto v){ return v>bi; });
        count += distance(begin(a), lba) * distance(begin(c), lbc);
    }
    
    cout << count;
}

Here is another snippet in python:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def triplets(a, b, c):
    a, b, c = map(lambda x: sorted(set(x)), (a, b, c))
    i_p = 0
    i_r = 0
    count = 0
    for q in b:
        while i_p < len(a) and a[i_p] <= q:
            i_p += 1
            
        while i_r < len(c) and c[i_r] <= q:
            i_r += 1
        
        count += i_p * i_r
    return count

Again, sorting the arrays is mandatory.