See the original problem on HackerRank.
The jedi apprentice Bin Logar is studying new lightsaber attack schemas for his year-end examination. In particular, he has found a secret technique to easily win duels when the battle takes place on uplands and small hills.
Bin is working out hard but his technique is still too slow because Bin needs to determine the maximum height of the battleground more quickly. For this reason you decide to help him.
Your task is to write a program that determines the peak of a battleground as fast as possible:
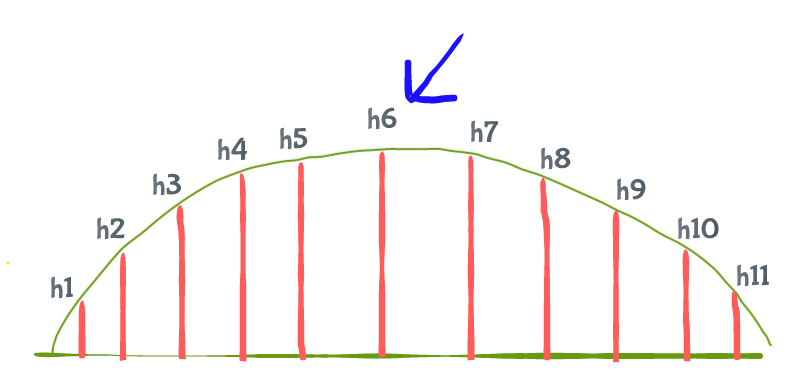
A battleground is given simply as a sequence of heights (h1, h2, etc) that are just integers that first increases and then decreases. You have to find the point which changes the direction of the battleground. Or, you have to find the maximum element as fast as possible.
Note:
The input of this challenge is a bit strange…let’s talk about that…
And don’t cheat :-)
Solutions
A clever solution is based on binary search:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
int FindPeak_BinarySearch(const vector<int>& arr, int low, int high, int n)
{
int mid = low + (high - low) / 2;
// Compare middle element with its neighbours (if neighbours exist)
if ((mid == 0 || arr[mid - 1] <= arr[mid]) &&
(mid == n - 1 || arr[mid + 1] <= arr[mid]))
return mid;
// If middle element is not peak and its left neighbour is greater
// than it, then left half must have a peak element
else if (mid > 0 && arr[mid - 1] > arr[mid])
return FindPeak_BinarySearch(arr, low, (mid - 1), n);
// If middle element is not peak and its right neighbour is greater
// than it, then right half must have a peak element
else return FindPeak_BinarySearch(arr, (mid + 1), high, n);
}
int FindPeak(const vector<int>& arr)
{
return arr[FindPeak_BinarySearch(arr, 0, arr.size() - 1, arr.size())];
}
int main()
{
int N, M, K;
cin >> N >> M >> K;
vector<int> v(N);
iota(begin(v), begin(v) + M, 0);
iota(v.rbegin(), v.rbegin() + v.size() - M, 0);
unsigned long long magicSum = 0;
for (auto i = 0; i < K; ++i)
magicSum+=FindPeak(v);
cout << magicSum;
}
|
